
Un reactor CSTR (Continuous Stirred Tank Reactor) es un tipo de reactor químico diseñado para realizar reacciones químicas en fase líquida o gaseosa de manera continua. A continuación, se describen sus características principales:
-
Mezcla Continua: El reactor CSTR mantiene una mezcla continua y uniforme de reactantes en su interior. Esto se logra mediante el uso de un sistema de agitación, como una hélice o una paleta, que garantiza la dispersión constante de los reactantes.
-
Entrada y Salida Continuas: A diferencia de un reactor por lotes, en un CSTR, los reactantes entran y salen continuamente durante todo el proceso. Esto permite una operación ininterrumpida y la producción constante de productos.
-
Condiciones Homogéneas: La mezcla constante asegura que las condiciones dentro del reactor, como la temperatura y la concentración, sean prácticamente uniformes en todo el volumen del reactor.
-
Control de Variables: Se pueden controlar y ajustar varias variables, como la temperatura, la presión y las tasas de flujo de entrada y salida, para optimizar las condiciones de reacción.
-
Aplicaciones Versátiles: Los reactores CSTR son versátiles y se utilizan en una amplia variedad de procesos industriales, incluyendo la síntesis química, la producción de productos químicos, la fermentación en la industria alimentaria, y más.
-
Tiempo de Residencia: El tiempo que un reactante pasa dentro del reactor, conocido como tiempo de residencia, es crucial para determinar la eficiencia de la reacción. Este tiempo de residencia se puede ajustar controlando el flujo de entrada y salida.
-
Eficiencia de Mezcla: La eficiencia de mezcla es una característica importante del CSTR, ya que una mezcla rápida y homogénea mejora la eficacia de la reacción y evita la formación de gradientes de concentración.
-
Modelado Matemático: Los reactores CSTR se describen a menudo mediante ecuaciones diferenciales que tienen en cuenta la cinética de la reacción y las condiciones de operación. Esto ayuda a comprender y predecir el comportamiento del reactor.
En resumen, un reactor CSTR es una herramienta fundamental en la ingeniería química para llevar a cabo reacciones químicas de manera continua y controlada, proporcionando flexibilidad y eficiencia en una variedad de aplicaciones industriales.
El contenido del reactor está prefectamente agitado y su composición es la misma en cada instante en todos los puntos del reactor. La corriente de salida de este reactor tiene la misma composición que la del fluido contenido en el mismo.
- $c_{A0}$: concentración inicial del reactivo A ($mol/m^3$).
- $x_{A0}$: conversión inicial. \item $Q_v$: caudal volumétrico ($m^3/s$).
- $F_{A0}$: flujo molar de reactivo A a la entrada (mol/s).
- $F_{A0}=c_{A0}Q_v$
- Reacción $A\rightarrow P$ con velocidad $(-r_A)$.
Balance de materia al reactor: Acumulación = Entrada - Salida - Desaparición
- Acumulación de A = 0 (No hay acumulación, todo lo que entra sale)
- Entrada de A = $F_{A0}$
- Salida de $A = F_{A}=F_{A0}(1-x_A)$
- Desaparición de A por reacción = $(-r_A)V$
Sustituyendo en el balance de materia:
\begin{equation} 0=F_{A0}-F_{A0}(1-x_A)-(-r_A)V \end{equation}
Simplificando esta última expresión, obtenemos la ecuación de diseño del CSTR
\begin{equation} \frac{V}{F_{A0}}=\frac{x_A}{(-r_A)} \end{equation}
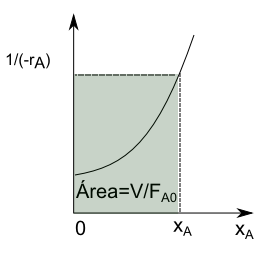
En sistemas de densidad constante, $c_A=c_{A0}(1-x_a)$, despejando $x_A$, $x_A=\frac{c_{A0}-c_A}{c_{A0}}$.
La ecuación de diseño nos queda,
\begin{equation} \frac{V}{F_{A0}}=\frac{c_{A0}-c_A}{(-r_A)c_{A0}}\;\rightarrow\;\frac{Vc_{A0}}{F_{A0}}=\frac{c_{A0}-c_A}{(-r_A)} \end{equation}
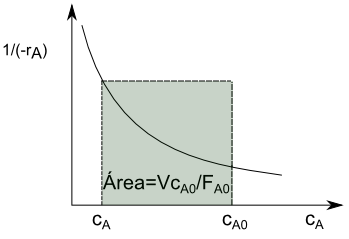
Tiempo espacial y velocidad espacial
Se define el tiempo espacial $\tau$ como el tiempo necesario para tratar un volumen de alimentación igual al volumen del reactor.
\begin{equation} \tau=\frac{V}{Q_v}=\frac{Vc_{A0}}{F_{A0}} \end{equation}
Se define la velocidad espacial (S) como el número de volúmenes de alimentación que pueden tratarse en la unidad de tiempo, medidos en volúmenes de reactor. La velocidad espacial es la inversa del tiempo espacial.
\begin{equation} S=\frac{1}{\tau} \end{equation}
El reactor CSTR (Continuous Stirred Tank Reactor) es utilizado en una variedad de reacciones químicas en las que se busca una operación continua y controlada. Algunos ejemplos de reacciones a las que se puede aplicar un CSTR incluyen:
-
Reacciones de Síntesis Química:
- Producción de productos químicos básicos.
- Síntesis de compuestos orgánicos.
- Fabricación de polímeros.
-
Reacciones de Fermentación:
- Producción de productos alimenticios, como fermentación de productos lácteos.
- Fermentación para la producción de productos químicos, como ácido láctico.
-
Reacciones de Biorremediación:
- Descomposición de contaminantes ambientales por microorganismos.
-
Reacciones de Neutralización:
- Neutralización de ácidos y bases para la producción de sales.
-
Reacciones de Hidrólisis:
- Hidrólisis de ésteres para la producción de alcoholes y ácidos.
-
Reacciones de Esterificación:
- Síntesis de ésteres a partir de ácidos y alcoholes.
-
Reacciones de Polimerización:
- Polimerización de monómeros para la producción de polímeros.
-
Reacciones de Descomposición Térmica:
- Descomposición de compuestos mediante calor.
-
Reacciones de Intercambio Iónico:
- Intercambio de iones en soluciones acuosas.
-
Reacciones de Oxidación-Reducción:
- Oxidación o reducción de compuestos químicos.
-
Reacciones de Hidrogenación:
- Hidrogenación de compuestos insaturados.
Estos son solo ejemplos, y la aplicabilidad del CSTR puede variar según las condiciones específicas de cada reacción y los requisitos del proceso. El diseño y la operación eficientes del CSTR dependen de factores como la cinética de la reacción, las propiedades de los reactantes y productos, y las condiciones de operación deseadas.


