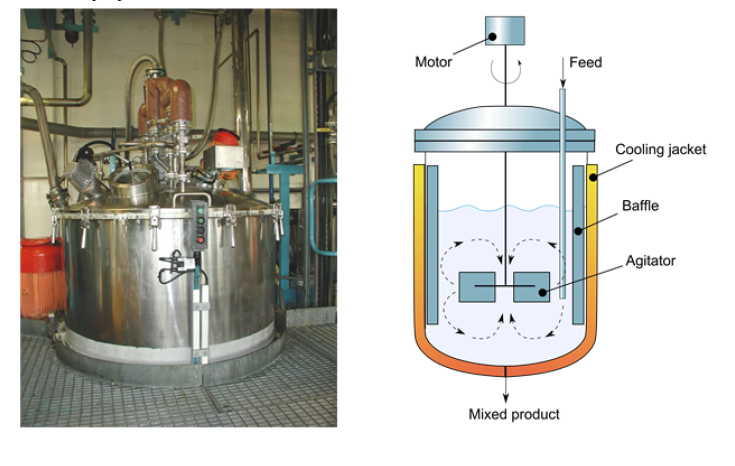
A discontinuous ideal reactor, also known as a batch reactor, is a type of chemical reactor in which reactants are loaded into the reactor, the reaction is allowed to occur for a specific period, and then the resulting product is discharged. This type of reactor operates in a batch cycle, meaning there is an initial loading of reactants, followed by a reaction period, and finally, the discharge of the product.
Key features of a discontinuous ideal reactor:
-
Batch Loading: Reactants are introduced into the reactor in a finite quantity at the beginning of each operating cycle.
-
Batch Operation: The chemical reaction occurs for a finite and predefined period.
-
Product Discharge: After completing the reaction, the product is removed from the reactor.
-
No Input or Output During Reaction: During the reaction period, no new reactants are introduced, and no products are withdrawn.
-
Condition Control: Conditions such as temperature and pressure can be controlled and adjusted during the reaction process.
-
Flexibility: This type of reactor is suitable for processes that require specific conditions during the reaction and can benefit from batch production.
It is important to note that, although the discontinuous ideal reactor provides some flexibility and control in production, it is not suitable for processes requiring continuous and constant production. Additionally, the total operation time includes both reaction time and loading/unloading time, which can impact the efficiency of the process compared to continuous flow reactors.
The reactants are introduced into the reactor, mixed, allowed to react for a certain time, and finally, the resulting mixture is discharged. The composition varies over time but is uniform throughout the reactor.
Material balance on the reactor:
Input = Output + Disappearance + Accumulation
- Input = Output = 0
- Disappearance of A by reaction: $(-r_A)V$
- Accumulation of A: $N_A=N_{A0}(1-x_A)$, differentiating with respect to t, $\frac{dN_A}{dt}=-N_{A0}\frac{dx_A}{dt}$
Substituting into the material balance:
\begin{equation} 0=(-r_A)V-N_{A0}\frac{dx_A}{dt} \end{equation}
Separating variables:
\begin{equation} dt=N_{A0}\frac{dx_A}{(-r_A)V}\;\rightarrow\;\int_{0}^{t}dt=N_{A0}\int_{0}^{x_A}\frac{dx_A}{(-r_A)V} \end{equation}
The design equation for a BR is then:
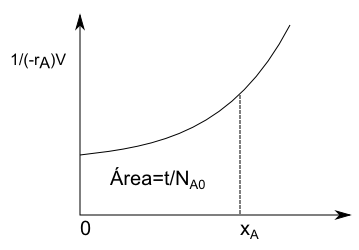
\begin{equation} t=N_{A0}\int_{0}^{x_A}\frac{dx_A}{(-r_A)V} \end{equation}
When the density does not change, i.e., the volume does not change:
\begin{equation} t=\frac{N_{A0}}{V}\int_{0}^{x_A}\frac{dx_A}{(-r_A)}=\frac{N_{A0}}{V}\int_{c_A0}^{c_A}\frac{-dc_A}{c_{A0}(-r_A)}=-\int_{c_{A0}}^{c_A}\frac{dc_A}{(-r_A)} \end{equation}
In the transition from the first to the second equality, we used: $c_A=c_{A0}(1-x_A)\;\rightarrow\;dc_A=-c_{A0}dx_A\;\rightarrow\;dx_A=-\frac{dc_A}{c_{A0}}$