A Piston Flow Reactor (PFR) or Tubular Flow Reactor is a type of chemical reactor in which reactants flow continuously through a tube or a system of pipes, and chemical reactions occur as the reactants move through the reactor. This type of reactor is characterized by having a constant and stationary flow of reactants through the system.
Here are some key features of a PFR:
-
Continuous Flow: Unlike other types of reactors, such as batch reactors, in a PFR, reactants continuously enter the system, and products are continuously extracted.
-
Residence Time Distribution: The time a reactant spends inside the reactor, known as residence time, varies along the reactor. Each reactant particle has a different residence time, allowing for a distribution of residence time.
-
Concentration Profile: Due to the constant flow, the concentration profile along the reactor changes as reactants react and convert into products. This contrasts with an ideal piston flow reactor, where the concentration of reactants remains constant in any cross-sectional area of the reactor.
-
Steady-State Reactions: Under ideal conditions, the PFR operates in a steady state, meaning that the system properties do not change over time. However, practical situations may lead to variations in reactor conditions.
-
Applications: PFRs are used in various industrial applications, such as chemical synthesis, pharmaceutical product manufacturing, polymer synthesis, and other chemical reactions on an industrial scale.
It is important to note that while the ideal piston flow reactor model is often used for theoretical and design purposes, in practice, PFRs may deviate from this ideal model due to factors such as imperfect mixing and variability in operating conditions.
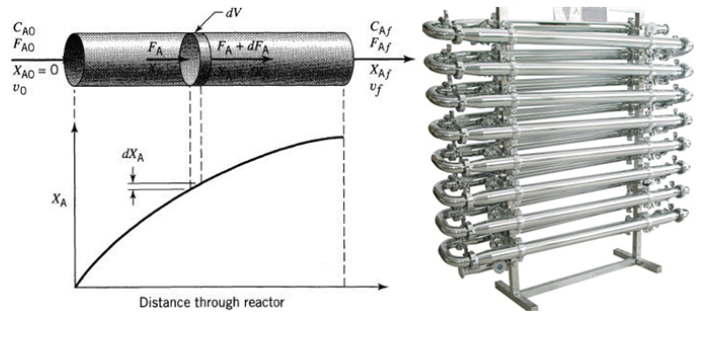
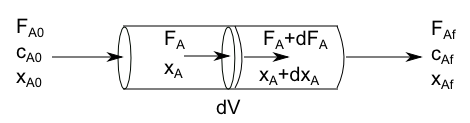
As the reactant moves along the reactor, the composition changes. We perform the material balance on the differential volume element and then extend it to the entire reactor.
Material balance: Accumulation = Inflow - Outflow - Disappearance
- Inflow of A in the dV: $F_A$
- Outflow of A from dV: $F_A+dF_A$
- Disappearance of A: $(-r_A)dV$
- Accumulation = 0
The material balance becomes $0=F_A-F_A+dF_A+(-r_a)dV$, given that $F_A=F_{A0}(1-x_A)$, differentiating, we get $dF_A=-F_{A0}dx_A$. Substituting this last equation into the material balance:
\begin{equation} F_{A0}dx_A=(-r_A)dV \end{equation}
Separating variables and integrating:
\begin{equation} \int_{0}^{v}\frac{dV}{F_{A0}}=\int_{0}^{x_{Af}}\frac{dx_A}{(-r_A)} \end{equation}
The PFR design equation is obtained:
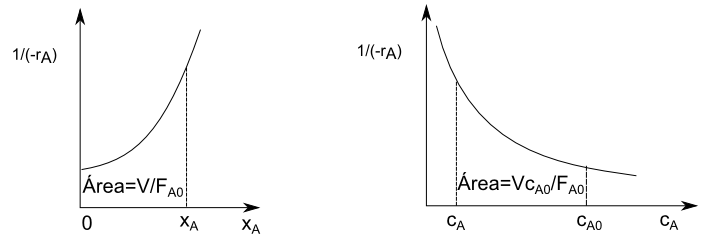
\begin{equation} \frac{V}{F_{A0}}=\int_{0}^{x_{Af}}\frac{dx_A}{(-r_A)} \end{equation}
It can also be expressed in terms of spatial time, considering that $\tau=\frac{c_{A0}V}{F_{A0}}$
\begin{equation} \tau=c_{A0}\int_{0}^{x_{Af}}\frac{dx_A}{(-r_A)} \end{equation}
In systems with constant density $c_A=C_{A0}(1-x_a)$, differentiating $dc_A=-c_{A0}dx_A$, solving for $dx_A=\frac{dx_A}{c_{A0}}$. Substituting $dx_A$ into the design equation yields:
\begin{equation} \tau=-\int_{c_{A0}}^{c_{Af}}\frac{dc_A}{(-r_A)} \end{equation}