- Detalles
- Escrito por: Germán Fernández
- Categoría: Balances de materia con reacción química
- Visto: 686
Mediante un proceso como el que se muestra en la figura, una sustancia A se convierte en B. Sabiendo que la conversión por paso es del 30%, calcular la cantidad de A que se recircula en el proceso.
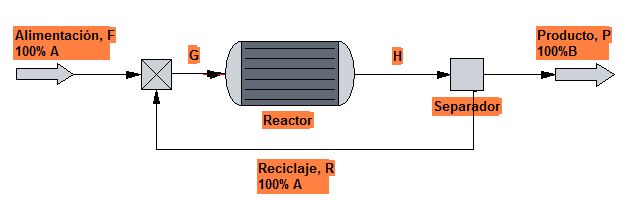
Solución:
Base de cálculo: 100 moles de alimentación.
Balance global total: $F=P\;\;\rightarrow P=100$
Balance local total al separador: $(F+R)\cdot 0.7=R\cdot 1 +P\cdot 0\;\;\rightarrow\;\; R=233\;moles$
- Detalles
- Escrito por: Germán Fernández
- Categoría: Balances de materia con reacción química
- Visto: 1464
En una planta se producen 800 t/día de amoniaco a partir de una mezcla estequiométrica de nitrógeno/hidrógeno, que contiene 0.15 moles de argon por cada 100 moles de mezcla $N_2/H_2$. En el reactor se alcanza una conversión del 25$\%$. El amoniaco producido condensa y los gases que no han reaccionado se recirculan al reactor. La concentración de argon a la entrada de éste, una vez mezcladas las corrientes de recirculación y de alimentación fresca, no debe ser superior a 3.5 moles/100 moles de mezcla $N_2/H_2$. Calcular:
a) Flujo molar de alimentación fresca
b) Flujo molar de la corriente de recirculación a la salida del condensador.
c) Flujo molar de la corriente de purga.
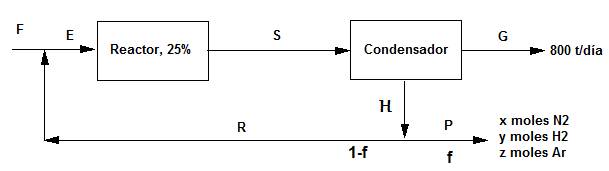
a) $9.69x10^{7}\;moles/día$; b) $2.67x10^8\;moles/día$; c) $2.46x10^6\; moles/día$
Respuesta:
Base de cálculo: 100 moles de $N_2/H_2$ en F.
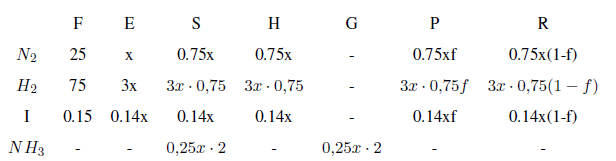
En la corriente A tenemos 3.5 moles de Ar por cada 100 moles de mezcla nitrógeno/hidrógeno. La fracción molar de Ar en esta corriente es: $3.5/103.5=0.0338$. Dicha fracción molar se puede igualar a $\frac{I}{4x+I}=0.0338$. Despejando los moles de inerte: $I=0.14x$
Balance local (punto de mezcla), parcial al nitrógeno:
$25+0.75x(1-f)=x$
Balance a los inertes en el punto de mezcla:
$0.15+0.14x(1-f)=0.14x$
Resolviendo el sistema: x= 97.57 y f=0.008
Amoniaco producido con la base de cálculo tomada: 0.5x=48.78 moles.
Transformamos en moles los 800 kg de amoniaco que se desean producir: $4.7x10^7$ moles.
Factor de escala: $\frac{4.7x10^7}{48.78}= 6.65x10^5\;dia^{-1}$
Multiplicando los datos de la tabla por el factor de escala se obtienen los flujos molares reales que circulan por el sistema.
Por ejemplo, $F=100.15\; mol x 9.65x10^5\;dia^{-1}= 9.69x10^7$ mol/día.
- Detalles
- Escrito por: Germán Fernández
- Categoría: Balances de materia con reacción química
- Visto: 943
Se ha despertado un interés considerable en la conversión de carbón en productos líquidos más útiles para la subsecuente producción de compuestos químicos. Dos de los principales gases que podemos generar en condiciones apropiadas a partir de la combustión de carbón in situ en presencia de vapor de agua (como sucede en presencia de aguas freáticas) son $H_2$ y CO. Después de lavarlos, estos dos gases se pueden combinar para producir metanol de acuerdo con la siguiente ecuación: $CO+2H_2\rightarrow CH_3OH$. Se usa un flujo de purgado para mantener la concentración de $CH_4$ en la salida del separador en no más de 3.2$\%$ mol. La conversión por paso de CO es del 18$\%$. Todas las composiciones están en fracciones molares o porcentajes molares. Los flujos están en moles. Calcular:
a) Los moles de reciclaje
b) Los moles de metanol producido
c) La cantidad purgada por mol de alimentación
d) La composición del gas de purga.
Solución:
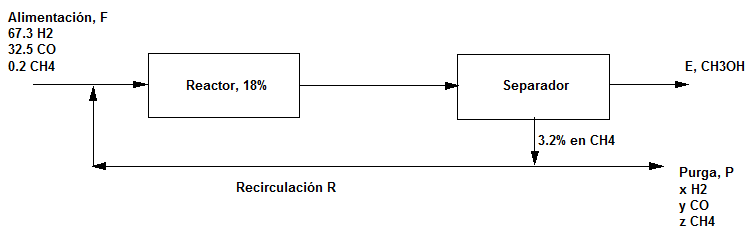
Base de cálculo 100: moles de alimentación.
Balance global parcial al H: $135.5=4E+2x+4z$
Balance global parcial al C: $32.5=y+z+E$
Balance global parcial al O: $32.5=E+y$
La corriente de purga contiene un 3.2$\%$ de $CH_4$, $z=0.032P$, es decir, $z=0.032(x+y+z)$.
Este sistema de cuatro ecuaciones nos permite calcular las cuatro incognitas, x,y,z,E.
x=4.8 moles; y=1.25 moles; z=0.2 moles; E=31.25 moles. La corriente de purga P=6.25 moles.
6.25 moles purgados/100 moles alimentados = 0.0625
Composición de la corriente de purga: $H_2$:76.8$\%$; CO: 20$\%$; $CH_4$:3.2$\%$.

Para obtener flujo molar recirculado hacemos un balance local (al punto de purga) y parcial (CO):
$(32.5+0.2R)(0.82)=0.2R+1.25$
R=705 moles


