- Detalles
- Escrito por: Germán Fernández
- Categoría: Reactores ideales
- Visto: 1246

Los reactores químicos son dispositivos o equipos utilizados en la industria química y en laboratorios para llevar a cabo reacciones químicas controladas. Estos dispositivos se diseñan específicamente para permitir que los reactivos se mezclen, reaccionen y produzcan productos químicos deseados de manera eficiente y controlada. Existen varios tipos de reactores químicos, y la elección del tipo adecuado depende de la naturaleza de la reacción y de los objetivos del proceso. A continuación, se describen algunos tipos comunes de reactores químicos:
1. Reactores de tanque agitado continuo (CSTR): En estos reactores, los reactivos se introducen continuamente en un tanque y se agitan de manera constante. La reacción ocurre en el tanque y los productos se retiran de manera continua. Los CSTR se utilizan en reacciones que requieren un tiempo de residencia constante y en procesos en estado estacionario.
2. Reactores de lecho fijo: En estos reactores, los reactivos fluyen a través de un lecho sólido catalítico o reactivo en estado sólido. Estos reactores se utilizan en procesos de catálisis heterogénea, como la craqueo de hidrocarburos en la industria petrolera.
3. Reactores de lecho fluidizado: En estos reactores, una corriente de gas se utiliza para mantener un lecho de partículas sólidas en suspensión. Se utilizan en procesos que involucran reacciones heterogéneas en fase gaseosa, como la síntesis de amoníaco.
- Detalles
- Escrito por: Germán Fernández
- Categoría: Reactores ideales
- Visto: 724
La velocidad de reacción $r_i$ se define como el número de moles consumidos o generados por unidad de tiempo y volumen de mezcla de reacción. \begin{equation} r_i=\frac{1}{V}\frac{dN_i}{dt} \end{equation}
En muchas reacciones químicas la velocidad de reacción puede escribirse como el producto de un factor dependiente de la temperatura (cte cinética) por otro dependiente de la concentración de reactivos.
- Detalles
- Escrito por: Germán Fernández
- Categoría: Reactores ideales
- Visto: 694
La conversión $x_A$ se define como la fracción del reactante A que es transformada en producto. Podemos obtener una expresión para la conversión a partir de la ecuación que nos da los moles de un reactivo A que no han reaccionado
$N_A=N_{A0}(1-x_A)\;\rightarrow x_A=\frac{N_{A0}-N_A}{N_{A0}}$.
También podemos expresar la conversión en función de concentraciones, $c_A=c_{A0}(1-x_A)$
- Detalles
- Escrito por: Germán Fernández
- Categoría: Reactores ideales
- Visto: 729
En reacciones gaseosas, se pueden producir variaciones de volumen a medida que la reacción transcurre. En esta situación utilizaremos una expresión simplificada que nos da el volumen en función de la conversión $V=V_0(1+\epsilon_Ax_A)$, donde $\epsilon_A$ es el factor de variación relativa de volumen del con la conversión del reactante A.
$\epsilon_A=\frac{V(x_A=1)-V(x_A=0)}{V(x_A=0)}$
Ejemplo del cálculo de $\epsilon_A$: Sea la reacción $A\rightarrow 4P$. Partimos de 1 mol inicial de A, cuando $x_A=1$ tendremos 4 moles de R. $\epsilon_A=\frac{4-1}{1}=3$.
- Detalles
- Escrito por: Germán Fernández
- Categoría: Reactores ideales
- Visto: 1134
La ley de Arrhenius da la dependencia de la constante de equilibrio con la temperatura. \begin{equation} k=Ae^{-E_a/RT} \end{equation} A, es el factor de frecuencia, relacionado con la frecuencia con que el complejo activado se descompone en los productos.
Donde:
- es la constante de velocidad de la reacción,
- es el factor preexponencial o factor de frecuencia,
- es la energía de activación de la reacción,
- es la constante de los gases ideales, y
- es la temperatura en kelvins.
Lee más: Ley de Arrhenius | Dependencia de la constante de equilibrio con la temperatura
- Detalles
- Escrito por: Germán Fernández
- Categoría: Reactores ideales
- Visto: 1114
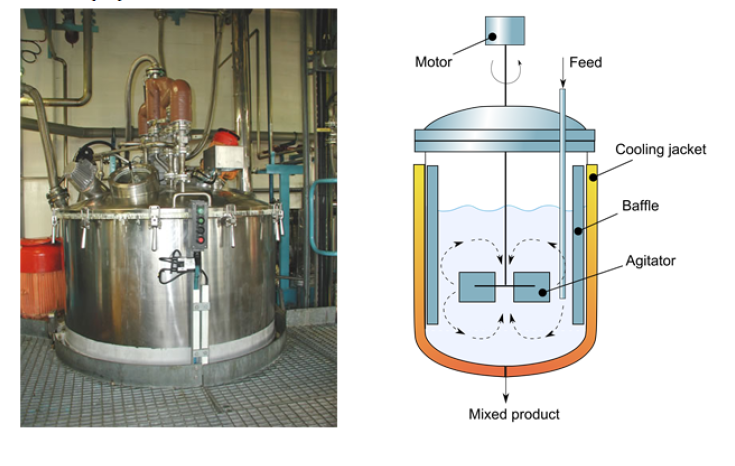
Un reactor ideal discontinuo, también conocido como reactor de lote o por lotes, es un tipo de reactor químico en el cual los reactantes se cargan en el reactor, se permite que ocurra la reacción por un período de tiempo específico y luego se descarga el producto resultante. Este tipo de reactor opera en un ciclo discontinuo, lo que significa que hay una carga inicial de reactantes, seguida de un período de reacción y, finalmente, la descarga del producto.
Características clave de un reactor ideal discontinuo:
-
Carga por lotes: Los reactantes se introducen en el reactor en una cantidad finita al comienzo de cada ciclo de operación.
-
Operación por lotes: La reacción química ocurre durante un tiempo finito y predefinido.
-
Descarga del producto: Después de completar la reacción, el producto se extrae del reactor.
-
No hay entrada ni salida durante la reacción: Durante el período de reacción, no se introducen nuevos reactantes ni se retiran productos.
-
Control de condiciones: Se pueden controlar y ajustar las condiciones, como la temperatura y la presión, durante el proceso de reacción.
-
Flexibilidad: Este tipo de reactor es adecuado para procesos que requieren condiciones específicas durante la reacción y que pueden beneficiarse de la producción en lotes.
Es importante destacar que, aunque el reactor ideal discontinuo proporciona cierta flexibilidad y control en la producción, no es adecuado para procesos que requieren una producción continua y constante. Además, el tiempo total de operación incluye tanto el tiempo de reacción como el tiempo de carga y descarga, lo que puede afectar la eficiencia del proceso en comparación con los reactores de flujo continuo.
Los reactantes se introducen en el reactor, se mezclan, se dejan que reaccionen un tiempo determinado y finalmente se descarga la mezcla resultante. La composición varía con el tiempo, aunque es uniforme en todo el reactor.
Balance de materia al reactor:
Entrada = Salida + Desaparición + Acumulación
- Entrada = Salida = 0
- Desaparición de A por reacción: $(-r_A)V$
- Acumulación de A: $N_A=N_{A0}(1-x_A)$, derivando respecto de t, $\frac{dN_A}{dt}=-N_{A0}\frac{dx_A}{dt}$
Sustuyendo en el balance de materia:
\begin{equation} 0=(-r_A)V-N_{A0}\frac{dx_A}{dt} \end{equation}
Separando variables:
\begin{equation} dt=N_{A0}\frac{dx_A}{(-r_A)V}\;\rightarrow\;\int_{0}^{t}dt=N_{A0}\int_{0}^{x_A}\frac{dx_A}{(-r_A)V} \end{equation}
La ecuación de diseño de un BR nos queda:
\begin{equation} t=N_{A0}\int_{0}^{x_A}\frac{dx_A}{(-r_A)V} \end{equation}
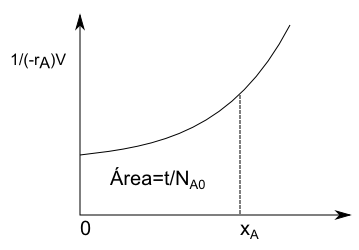
Lee más: Ecuación de diseño para un reactor ideal discontinuo (BR)
- Detalles
- Escrito por: Germán Fernández
- Categoría: Reactores ideales
- Visto: 3178

Un reactor CSTR (Continuous Stirred Tank Reactor) es un tipo de reactor químico diseñado para realizar reacciones químicas en fase líquida o gaseosa de manera continua. A continuación, se describen sus características principales:
-
Mezcla Continua: El reactor CSTR mantiene una mezcla continua y uniforme de reactantes en su interior. Esto se logra mediante el uso de un sistema de agitación, como una hélice o una paleta, que garantiza la dispersión constante de los reactantes.
-
Entrada y Salida Continuas: A diferencia de un reactor por lotes, en un CSTR, los reactantes entran y salen continuamente durante todo el proceso. Esto permite una operación ininterrumpida y la producción constante de productos.
-
Condiciones Homogéneas: La mezcla constante asegura que las condiciones dentro del reactor, como la temperatura y la concentración, sean prácticamente uniformes en todo el volumen del reactor.
-
Control de Variables: Se pueden controlar y ajustar varias variables, como la temperatura, la presión y las tasas de flujo de entrada y salida, para optimizar las condiciones de reacción.
-
Aplicaciones Versátiles: Los reactores CSTR son versátiles y se utilizan en una amplia variedad de procesos industriales, incluyendo la síntesis química, la producción de productos químicos, la fermentación en la industria alimentaria, y más.
-
Tiempo de Residencia: El tiempo que un reactante pasa dentro del reactor, conocido como tiempo de residencia, es crucial para determinar la eficiencia de la reacción. Este tiempo de residencia se puede ajustar controlando el flujo de entrada y salida.
-
Eficiencia de Mezcla: La eficiencia de mezcla es una característica importante del CSTR, ya que una mezcla rápida y homogénea mejora la eficacia de la reacción y evita la formación de gradientes de concentración.
-
Modelado Matemático: Los reactores CSTR se describen a menudo mediante ecuaciones diferenciales que tienen en cuenta la cinética de la reacción y las condiciones de operación. Esto ayuda a comprender y predecir el comportamiento del reactor.
En resumen, un reactor CSTR es una herramienta fundamental en la ingeniería química para llevar a cabo reacciones químicas de manera continua y controlada, proporcionando flexibilidad y eficiencia en una variedad de aplicaciones industriales.
El contenido del reactor está prefectamente agitado y su composición es la misma en cada instante en todos los puntos del reactor. La corriente de salida de este reactor tiene la misma composición que la del fluido contenido en el mismo.
- $c_{A0}$: concentración inicial del reactivo A ($mol/m^3$).
- $x_{A0}$: conversión inicial. \item $Q_v$: caudal volumétrico ($m^3/s$).
- $F_{A0}$: flujo molar de reactivo A a la entrada (mol/s).
- $F_{A0}=c_{A0}Q_v$
- Reacción $A\rightarrow P$ con velocidad $(-r_A)$.
Balance de materia al reactor: Acumulación = Entrada - Salida - Desaparición
- Acumulación de A = 0 (No hay acumulación, todo lo que entra sale)
- Entrada de A = $F_{A0}$
- Salida de $A = F_{A}=F_{A0}(1-x_A)$
- Desaparición de A por reacción = $(-r_A)V$
Sustituyendo en el balance de materia:
\begin{equation} 0=F_{A0}-F_{A0}(1-x_A)-(-r_A)V \end{equation}
Simplificando esta última expresión, obtenemos la ecuación de diseño del CSTR
\begin{equation} \frac{V}{F_{A0}}=\frac{x_A}{(-r_A)} \end{equation}
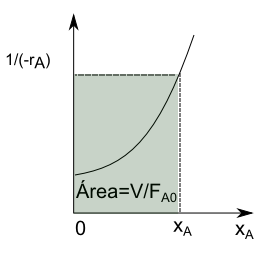
Lee más: Ecuación de diseño de un reactor ideal continuo de mezcla completa (CSTR)
- Detalles
- Escrito por: Germán Fernández
- Categoría: Reactores ideales
- Visto: 4799
Un reactor PFR (Reactor de Flujo Pistón o Reactor de Flujo Tubular) es un tipo de reactor químico en el que los reactantes fluyen continuamente a través de un tubo o un sistema de tuberías, y las reacciones químicas ocurren mientras los reactantes se desplazan a través del reactor. Este tipo de reactor se caracteriza por tener un flujo constante y estacionario de reactantes a través del sistema.
Aquí hay algunas características clave de un reactor PFR:
-
Flujo Continuo: A diferencia de otros tipos de reactores, como el reactor por lotes, en un reactor PFR los reactantes ingresan continuamente al sistema y los productos se extraen de manera continua.
-
Distribución de Tiempo de Residencia: El tiempo que un reactante pasa dentro del reactor, conocido como tiempo de residencia, varía a lo largo del reactor. Cada partícula de reactante tiene un tiempo diferente de permanencia en el reactor, lo que permite una distribución de tiempo de residencia.
-
Perfil de Concentración: Debido al flujo constante, el perfil de concentración a lo largo del reactor cambia a medida que los reactantes reaccionan y se convierten en productos. Esto contrasta con un reactor de flujo de pistón ideal, donde la concentración de los reactantes permanece constante en cualquier sección transversal del reactor.
-
Reacciones en Estado Estacionario: En condiciones ideales, el reactor PFR opera en estado estacionario, lo que significa que las propiedades del sistema no cambian con el tiempo. Sin embargo, en situaciones prácticas, pueden existir variaciones en las condiciones del reactor.
-
Aplicaciones: Los reactores PFR se utilizan en una variedad de aplicaciones industriales, como la síntesis química, la producción de productos farmacéuticos, la síntesis de polímeros y otras reacciones químicas a escala industrial.
Es importante destacar que, aunque el modelo ideal de reactor de flujo de pistón se utiliza a menudo para fines teóricos y de diseño, en la práctica, los reactores PFR pueden presentar desviaciones de este modelo ideal debido a factores como la mezcla imperfecta y la variabilidad en las condiciones de operación.
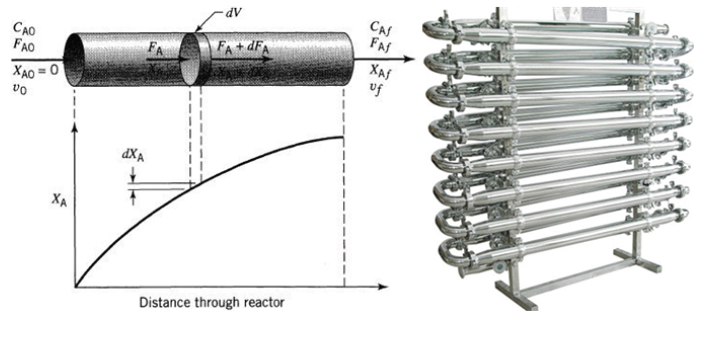
Lee más: Ecuación de diseño de un reactor ideal de flujo de pistón (PFR)


