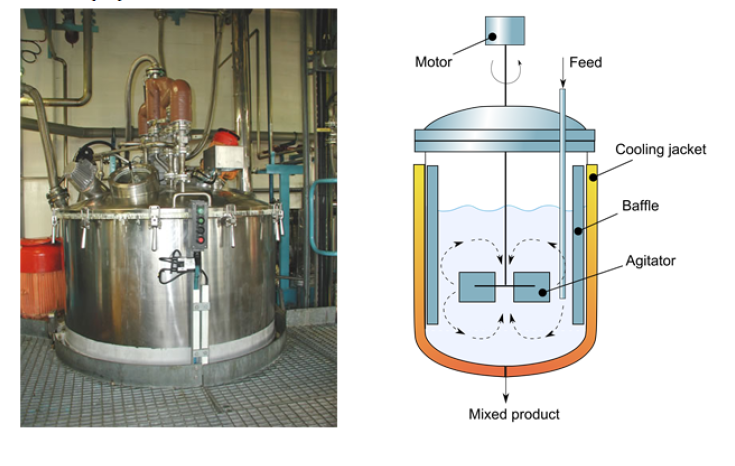
Un reactor ideal discontinuo, también conocido como reactor de lote o por lotes, es un tipo de reactor químico en el cual los reactantes se cargan en el reactor, se permite que ocurra la reacción por un período de tiempo específico y luego se descarga el producto resultante. Este tipo de reactor opera en un ciclo discontinuo, lo que significa que hay una carga inicial de reactantes, seguida de un período de reacción y, finalmente, la descarga del producto.
Características clave de un reactor ideal discontinuo:
-
Carga por lotes: Los reactantes se introducen en el reactor en una cantidad finita al comienzo de cada ciclo de operación.
-
Operación por lotes: La reacción química ocurre durante un tiempo finito y predefinido.
-
Descarga del producto: Después de completar la reacción, el producto se extrae del reactor.
-
No hay entrada ni salida durante la reacción: Durante el período de reacción, no se introducen nuevos reactantes ni se retiran productos.
-
Control de condiciones: Se pueden controlar y ajustar las condiciones, como la temperatura y la presión, durante el proceso de reacción.
-
Flexibilidad: Este tipo de reactor es adecuado para procesos que requieren condiciones específicas durante la reacción y que pueden beneficiarse de la producción en lotes.
Es importante destacar que, aunque el reactor ideal discontinuo proporciona cierta flexibilidad y control en la producción, no es adecuado para procesos que requieren una producción continua y constante. Además, el tiempo total de operación incluye tanto el tiempo de reacción como el tiempo de carga y descarga, lo que puede afectar la eficiencia del proceso en comparación con los reactores de flujo continuo.
Los reactantes se introducen en el reactor, se mezclan, se dejan que reaccionen un tiempo determinado y finalmente se descarga la mezcla resultante. La composición varía con el tiempo, aunque es uniforme en todo el reactor.
Balance de materia al reactor:
Entrada = Salida + Desaparición + Acumulación
- Entrada = Salida = 0
- Desaparición de A por reacción: $(-r_A)V$
- Acumulación de A: $N_A=N_{A0}(1-x_A)$, derivando respecto de t, $\frac{dN_A}{dt}=-N_{A0}\frac{dx_A}{dt}$
Sustuyendo en el balance de materia:
\begin{equation} 0=(-r_A)V-N_{A0}\frac{dx_A}{dt} \end{equation}
Separando variables:
\begin{equation} dt=N_{A0}\frac{dx_A}{(-r_A)V}\;\rightarrow\;\int_{0}^{t}dt=N_{A0}\int_{0}^{x_A}\frac{dx_A}{(-r_A)V} \end{equation}
La ecuación de diseño de un BR nos queda:
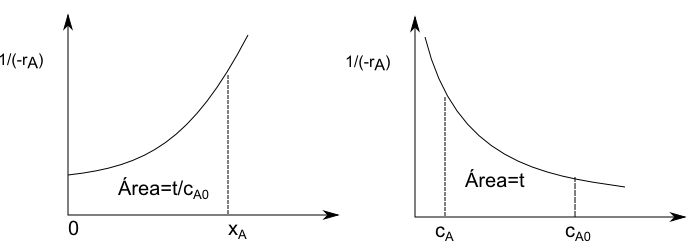
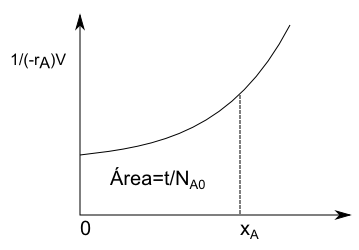
\begin{equation} t=N_{A0}\int_{0}^{x_A}\frac{dx_A}{(-r_A)V} \end{equation}
Cuando la densidad no varía, es decir, el volumen no cambia:
\begin{equation} t=\frac{N_{A0}}{V}\int_{0}^{x_A}\frac{dx_A}{(-r_A)}=\frac{N_{A0}}{V}\int_{c_A0}^{c_A}\frac{-dc_A}{c_{A0}(-r_A)}=-\int_{c_{A0}}^{c_A}\frac{dc_A}{(-r_A)} \end{equation}
En el paso de la primera a la segunda igualdad hemos utilizado: $c_A=c_{A0}(1-x_A)\;\rightarrow\;dc_A=-c_{A0}dx_A\;\rightarrow\;dx_A=-\frac{dc_A}{c_{A0}}$