- Details
- Written by: Germán Fernández
- Category: Balances de materia sin reacción
- Hits: 89
Balance de materia de un proceso industrial es una contabilidad exacta de todos los materiales que entran, salen, se acumulan o se agotan en un intervalo de operaciòn dado.
Se pueden distinguir cuatro tipos de balances de materia dependiendo del tipo de sistema:
- Acumulación = Entrada - Salida + Generación - Consumo.
Es un sistema con entradas, salidas y reacciones químicas.
- Acumulación = Entrada - Salida.
Sistema sin reacciones químicas.
- Entrada = Salida.
Sistema en estado estacionario, no hay acumulación ni reacciones químicas.
- Acumulación = Generación - Consumo.
Sistema sin corrientes de entrada ni de salida, pero con reacción química.
Tipos de sistemas
Se llama sistema a cualquier porción arbitraria o completa de un proceso. Los sistemas se clasifican en:
- Sistema abierto o contínuo: es aquel en el que la materia se transfiere a través de la frontera del sistema; es decir, entra en el sistema, o sale de él, o ambas cosas.
- Sistema cerrado o por lotes: es aquel en el que no hay transferencia de materia a través de la frontera del sistema.
- Details
- Written by: Germán Fernández
- Category: Balances de materia sin reacción
- Hits: 79
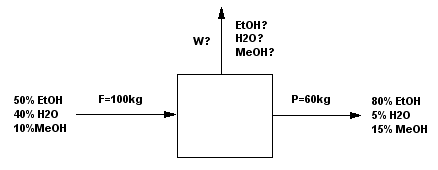
Tenemos una corriente F de 100 kg formada por 50 de EtOH, 40 de $H_{2}O$ y 10 de MeOH. Sale una corriente P de 60kg, formada por 80 EtOH, 5 $H_{2}O$ y 15 MeOH. ¿Cuál es el valor de la corriente W y su composición?
Para resolver el problema comenzamos escribiendo el balance de masas total.
Entrada = Salida \begin{equation} 100 = 60 + W\ \longrightarrow W=40\ kg \end{equation} Sea $w_iF$ la fracción másica del componente $i$ en la corriente F. Haciendo un balance de masas al componente $i$: \begin{equation} w_{iF}F=w_{iP}P+w_{iw}W \end{equation} Planteando este balance de materia para todos los componentes nos da: \begin{equation} EtOH:\ (0,50)(100)=(0,8)(60)+w_{EtOH,w}W \end{equation} \begin{equation} H_{2}O:\ (0,40)(100)=(0,05)(60)+w_{H_{2}O,w}W \end{equation} \begin{equation} MeOH:\ (0,10)(100)=(0,15)(60)+w_{MeOH,w}W \end{equation} La suma de estas tres ecuaciones da el balance global. Por tanto, estas cuatro ecuaciones no son independientes y no son suficientes para el cálculo de las cuatro incognicas. Necesitamos una ecuación más que sea independiente. \begin{equation} w_{EtOH}+w_{H_{2}O}+w_{MeOH}=1 \end{equation} Esta útima ecuación indica que la suma de fracciones másicas para todos los componentes e una corriente es la unidad.
- Details
- Written by: Germán Fernández
- Category: Balances de materia sin reacción
- Hits: 76
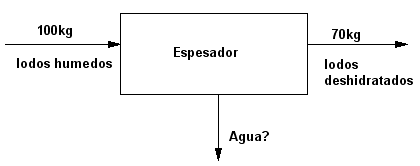
Calcular los Kg de agua que salen de un espesador, al que entran 100 kg de lodos húmedos, obteniéndose 70 kg de lodos deshidratados.
Primero se dibuja el diagrama de flujo del sistema.
En el espesador no hay acumulación de materia ni reacción química. El balance de materia al espesador puede escribirse como:
Entrada = Salida
100kg = 70 + x
x = 100 - 70 =30 kg de agua
- Details
- Written by: Germán Fernández
- Category: Balances de materia sin reacción
- Hits: 72
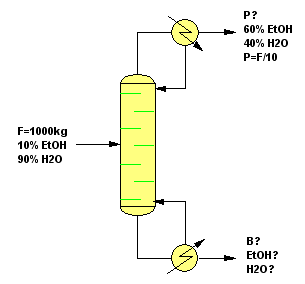
Obtener la masa y composición de las corrientes P y B sabiendo que la relación entre la corriente de alimentación y destilado es de 10.
Sabemos que la corriente de destilado es la decima parte de la alimentación. \begin{equation} P=\frac{F}{10}=\frac{1000\ kg}{10}=100\ kg \end{equation} Aplicando un balance de materia total: \begin{equation} 1000=100+B\ \longrightarrow\ B=900\ kg \end{equation} Aplicando balances de materia a etanol y agua se obtiene su fracción másica en la corriente B. \begin{equation} EtOH:\ (0.10)(1000)=(0,60)(100)+W_{EtOH,B}(900)\longrightarrow\ W_{EtOH,B}=0,044 \end{equation} \begin{equation} H_{2}O:\ (0,9)(1000)=(0,40)(100)+W_{H_{2}O,B}(900)\longrightarrow\ W_{H_{2}O,B}=0,956 \end{equation}
- Details
- Written by: Germán Fernández
- Category: Balances de materia sin reacción
- Hits: 81
Calcula las corrientes F y P
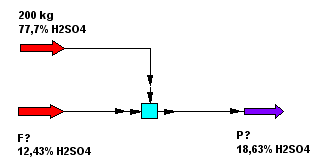
Es un problema con dos incognitas F y P. Para resolverlo buscamos dos ecuaciones independientes: balance de materia global y balance al ácido sulfúrico. \begin{equation} 200+F=P \end{equation} \begin{equation} (0,777)(200)+(0,1243)F=(0,1863)P \end{equation} La solución del sistema nos da: F= 1910 kg, P = 2110 kg.
Se puede comprobar que la solución es correcta haciendo un balance al agua.
- Details
- Written by: Germán Fernández
- Category: Balances de materia sin reacción
- Hits: 112
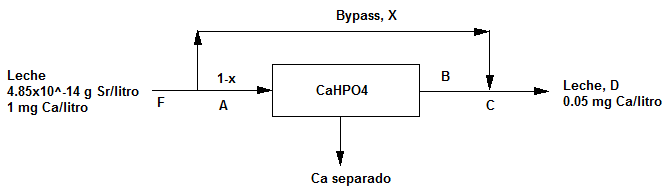
Determinar las corrientes A, B, C, P y W, así como las composiciones wKCl,A y wH2O,A
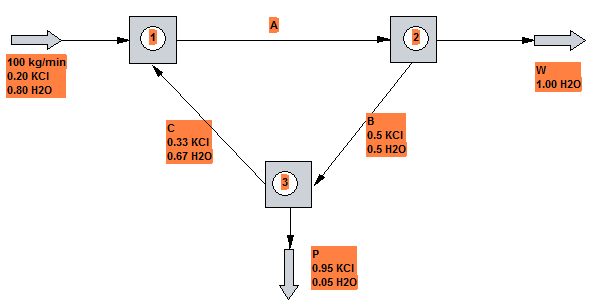
Cuando en un problema de balances de materia tenemos varios subsistemas aplicaremos dos tipos de balance:
- Balance de materia a todo el sistema.
- Balance de materia a cada subsistema.
Debe tenerse encuenta que la ecuación que resulta del balance total es dependiente de las ecuaciones obtenidas por balance a los diferentes subsistemas.
- Balance de masa a todo el sistema: $100=P+W$
Balance al KCl: $(0.20)\cdot(100)=0.91P$
- Balance a la unidad 1: $100+C=A$
Balance al KCl : $(0.20)\cdot(100)+0.33C=w_{KCl,A}A$
- Balance a la unidad 2: $A=B+W$
Balance al KCl:$ w_{KCl,A}A=0.50B$
Podemos escribir una última ecuación para la corriente A: $w_{KCl,A}+w_{H2O,A}=1$
Hemos planteado 7 ecuaciones independientes que permiten por resolución del sistema obtener las 7 incognitas.
- Details
- Written by: Germán Fernández
- Category: Balances de materia sin reacción
- Hits: 76
El componente de enlace es un material que pasa de una corriente a otra sin sufrir cambios. Una vez identificado el componente de enlace puede escribirse un balance de materia que incluya solo las dos corrientes que lo contienen.
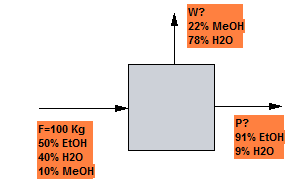
Tanto el metanol como el etanol pueden emplearse como componetes de enlace por estar en dos de las corrientes. Sin embargo, el agua no es un componente de enlace ya que está presente en las tres corrientes.
Tomando como componente de enlace el metanol, podemos escribir \begin{equation} w_{MeOH,F}F=w_{MeOH,W}W\;\;\rightarrow\;\; (0.10)\cdot(100)=0.22W\;\;\rightarrow \;\;W=45.5\;kg \end{equation}
- Details
- Written by: Germán Fernández
- Category: Balances de materia sin reacción
- Hits: 105
Recirculación: parte de la corriente que sale de un proceso se incorpora de nuevo el proceso
Veamos algunos ejemplos:
- En procesos de secado se controla la humedad recirculando parte del aire húmedo que sale del secadero.
- En reacciones químicas el material que no ha reaccionado se separa y se recircula al reactor.
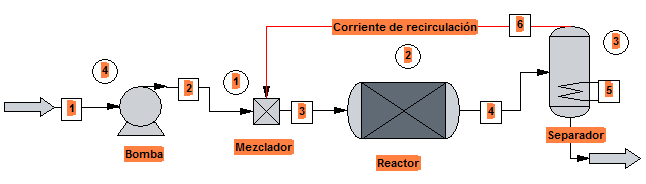
- Las columnas de destilación con rectificación, recirculan parte del destilado
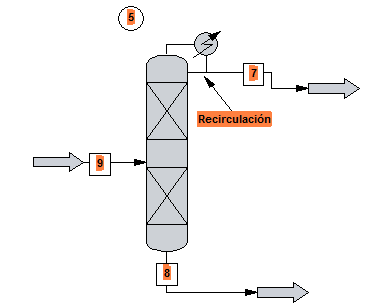
Derivación "by pass": corriente que pasa por alto una o más etapas del proceso, llegándo directamente a otra etapa posterior
Purga: Corriente que se utiliza para eliminar una acumulación de sustancias inertes o indeseables que de otra manera se acumularían en el flujo de recirculación.
- Details
- Written by: Germán Fernández
- Category: Balances de materia sin reacción
- Hits: 194
Supóngase que en una planta de desalinización de ósmosis inversa se tratan 4000 kg/h de una disolución salina con un 4 % en peso de sal, y que las condiciones de operación son tales que se obtienen 1200 kg/h de agua desalinizada con un 0.3 % en peso de sales.
Calcular:
a) El caudal volumétrico;
b) La salinidad de la salmuera de rechazo.
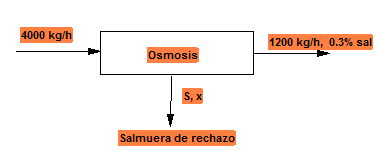
Balance global total: 4000 = 1200 + S
S=2800 kg/h
Balance global parcial a la sal: $4000\cdot 0.04=1200\cdot 0.003 + S\cdot X$
X=0.0558
- Details
- Written by: Germán Fernández
- Category: Balances de materia sin reacción
- Hits: 226
Considérese un sistema evaporador y cristalizador como el del esquema. En él se tratan 10000 kg/h de una disolución que contiene 20 % de sólido en peso. La disolución concentrada con un 50 % en peso de sólidos que sale del evaporador se lleva al cristalizador donde se enfría, cristalizando el sólido y extrayéndose los cristales con un 4% de agua. La disolución saturada, conteniendo 0.6 kg de sólido/kg de agua, se recircula, incorporándose a la corriente de alimento del evaporador. Calcular los flujos másicos:
a) Sal húmeda producida;
b) Disolución recirculada;
c) Agua evaporada.
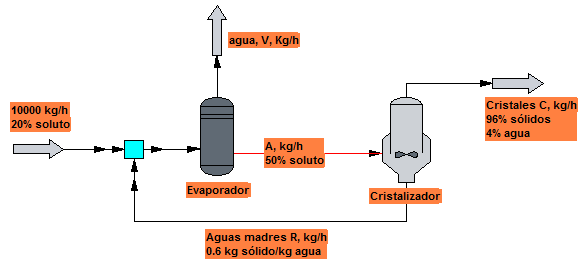
Solución:
Balance global total: $10000 = V + C\;\; \rightarrow\;\; V= 7917\;kg/h$
Balance global parcial (soluto): $10000\cdot 0.2 =C\cdot 0.96\;\; \rightarrow\;\; C=2083\; kg/h$
Balance local total (evaporador): $10000+R=A+V$
Balance local parcial (evaporador, soluto): $10000\cdot 0.2 =R\frac{0.6}{0.6+1}=A\cdot 0.5$
Resolviendo el sistema se obtiene A=9751 kg/h y R=7668 kg/h
- Details
- Written by: Germán Fernández
- Category: Balances de materia sin reacción
- Hits: 70
Se ha diseñado un evaporador para una alimentación de 11500 kg/día de zumo de pomelo de forma que evapore 3000 kg/día de agua y se obtenga una disolución concentrada al 50$\%$. ¿Con qué concentración inicial se deberá alimentar el zumo y qué cantidad de disolución concentrada al 50$\%$ se obtiene?.
Solución:
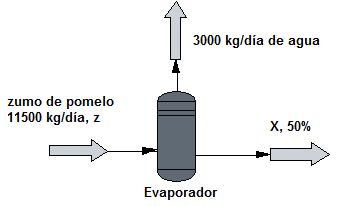
Balance global total: 11500 = 3000 + X
Balance global parcial (zumo): $11500\cdot z = 3000\cdot 0+X\cdot 0.5$
Resolviendo el sistema: x=8500 kg/día; z=0.3695.
- Details
- Written by: Germán Fernández
- Category: Balances de materia sin reacción
- Hits: 84
Una corriente de 1000 kg/h que contiene 10$\%$ de alcohol, 20$\%$ de azúcar y el resto de agua, se mezcla con 2000 kg/h de una corriente con 25$\%$ de alcohol, 50$\%$ de azúcar y el resto agua. ¿Cuál será la composición de la mezcla resultante?.
Solución:
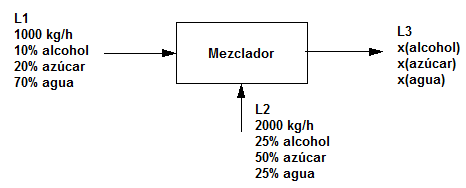
- Balance global total: $L_1 +L_2 =L_3\;\;\rightarrow\;\; L_3=3000\;kg/h$
- Balance global parcial (alcohol): $1000\cdot 0.1+2000\cdot 0.25 =3000\cdot x_{alcohol}\;\;\rightarrow\;\;x_{alcohol}=0.2$
- Balance global parcial (azúcar): $1000\cdot 0.2 +2000\cdot 0.5=3000\cdot x_{azucar}\;\;\rightarrow\;\;x_{azucar}=0.4$
- Details
- Written by: Germán Fernández
- Category: Balances de materia sin reacción
- Hits: 68
Sea el critalizador de la figura, al que se alimentan 5600 kg/h de una disolución salina caliente con una concentración de 50$\%$ en peso de sal. Al enfriar cristaliza la sal, separándose una disolución fría saturada con 20$\%$ en peso de sal y cristales húmedos con 5$\%$ en peso de agua. Calcular los caudales másicos de disolución saturada y de cristales húmedos que salen del cristalizador.
Solución:
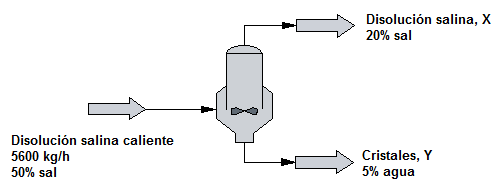
Balance global total: $5600=X+Y$
Balance global parcial (sal): $5600\cdot 0.5=X\cdot 0.2+Y\cdot 0.95$
Resolviendo el sistema: X=3360 kg/h; Y=2200 kg/h.
- Details
- Written by: Germán Fernández
- Category: Balances de materia sin reacción
- Hits: 93
Sea el evaporador de la figura, donde se concentran 10000 kg/h de una disolución salina diluida de 5% en peso hasta una concentración del 30% en peso. Calcular el caudal másico de agua evaporada.
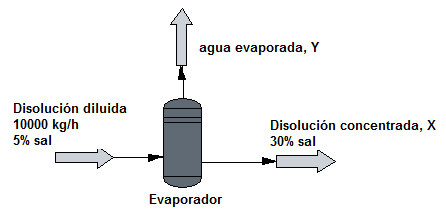
Solución:
- Details
- Written by: Germán Fernández
- Category: Balances de materia sin reacción
- Hits: 75
Una disolución acuosa de hidróxido de sodio contiene 20$\%$ en masa de NaOH. Se desea producir una disolución al 8$\%$ de NaOH diluyendo un flujo de una disolución al 20$\%$ con un flujo de agua pura.
a) Calcular los cocientes (g de $H_2O$/g de la disolución de alimentación) y (g de la disolución producto/g de la disolución de alimentación).
b) Determinar las velocidades de flujo de la disolución de alimentación y del agua de dilución necesarias para producir 2310 $lb_m/min$ de la disolución al 8$\%$
Solución:
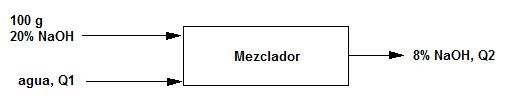
- Base de cálculo 100 g de disolución
- Balance global total: $100 + Q_1=Q_2$
- Balance global parcial $(NaOH): 100\cdot 0.2=Q_2\cdot 0.08$
- Resolviendo el sistema: $Q_2=250\;g$de NaOH y $Q_1=150\;g$ de agua.
a) 150 g de agua/100 g de alimentación = 1.5
- 250 g de disolución al 8$\%$/100 g de alimentación = 2.5
b) Utilizamos un factor de escala: $\frac{2310}{250}=9.24\;lb/gmin$
- lb/min de alimentación: 924
- lb/min de agua: 1386
- Details
- Written by: Germán Fernández
- Category: Balances de materia sin reacción
- Hits: 68
Se encontró que una pulpa húmeda de papel contenía 71$\%$ de agua. Después de secarla se encontró que se había eliminado el 60$\%$ del agua original. Calcular:
a) La cantidad de pulpa seca.
b) La masa de agua eliminada por kg e pulpa húmeda.
Solución:
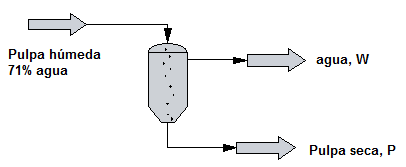
Base de cálculo 1 kg de pulpa. En 1 kg de pulpa húmeda tenemos 0.710 kg de agua, de los cuales se elimina el 60$\%$, equivalente a W=0.426 kg.
Balance global total: $1=0.426 + P\;\;\rightarrow\;\; P=0.574$ kg de pulpa seca.
- Details
- Written by: Germán Fernández
- Category: Balances de materia sin reacción
- Hits: 85
