Tenemos una corriente F de 100 kg formada por 50 de EtOH, 40 de $H_{2}O$ y 10 de MeOH. Sale una corriente P de 60kg, formada por 80 EtOH, 5 $H_{2}O$ y 15 MeOH. ¿Cuál es el valor de la corriente W y su composición?
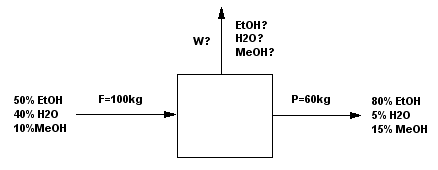
Para resolver el problema comenzamos escribiendo el balance de masas total.
Entrada = Salida \begin{equation} 100 = 60 + W\ \longrightarrow W=40\ kg \end{equation} Sea $w_iF$ la fracción másica del componente $i$ en la corriente F. Haciendo un balance de masas al componente $i$: \begin{equation} w_{iF}F=w_{iP}P+w_{iw}W \end{equation} Planteando este balance de materia para todos los componentes nos da: \begin{equation} EtOH:\ (0,50)(100)=(0,8)(60)+w_{EtOH,w}W \end{equation} \begin{equation} H_{2}O:\ (0,40)(100)=(0,05)(60)+w_{H_{2}O,w}W \end{equation} \begin{equation} MeOH:\ (0,10)(100)=(0,15)(60)+w_{MeOH,w}W \end{equation} La suma de estas tres ecuaciones da el balance global. Por tanto, estas cuatro ecuaciones no son independientes y no son suficientes para el cálculo de las cuatro incognicas. Necesitamos una ecuación más que sea independiente. \begin{equation} w_{EtOH}+w_{H_{2}O}+w_{MeOH}=1 \end{equation} Esta útima ecuación indica que la suma de fracciones másicas para todos los componentes e una corriente es la unidad.


