Un reactor PFR (Reactor de Flujo Pistón o Reactor de Flujo Tubular) es un tipo de reactor químico en el que los reactantes fluyen continuamente a través de un tubo o un sistema de tuberías, y las reacciones químicas ocurren mientras los reactantes se desplazan a través del reactor. Este tipo de reactor se caracteriza por tener un flujo constante y estacionario de reactantes a través del sistema.
Aquí hay algunas características clave de un reactor PFR:
-
Flujo Continuo: A diferencia de otros tipos de reactores, como el reactor por lotes, en un reactor PFR los reactantes ingresan continuamente al sistema y los productos se extraen de manera continua.
-
Distribución de Tiempo de Residencia: El tiempo que un reactante pasa dentro del reactor, conocido como tiempo de residencia, varía a lo largo del reactor. Cada partícula de reactante tiene un tiempo diferente de permanencia en el reactor, lo que permite una distribución de tiempo de residencia.
-
Perfil de Concentración: Debido al flujo constante, el perfil de concentración a lo largo del reactor cambia a medida que los reactantes reaccionan y se convierten en productos. Esto contrasta con un reactor de flujo de pistón ideal, donde la concentración de los reactantes permanece constante en cualquier sección transversal del reactor.
-
Reacciones en Estado Estacionario: En condiciones ideales, el reactor PFR opera en estado estacionario, lo que significa que las propiedades del sistema no cambian con el tiempo. Sin embargo, en situaciones prácticas, pueden existir variaciones en las condiciones del reactor.
-
Aplicaciones: Los reactores PFR se utilizan en una variedad de aplicaciones industriales, como la síntesis química, la producción de productos farmacéuticos, la síntesis de polímeros y otras reacciones químicas a escala industrial.
Es importante destacar que, aunque el modelo ideal de reactor de flujo de pistón se utiliza a menudo para fines teóricos y de diseño, en la práctica, los reactores PFR pueden presentar desviaciones de este modelo ideal debido a factores como la mezcla imperfecta y la variabilidad en las condiciones de operación.
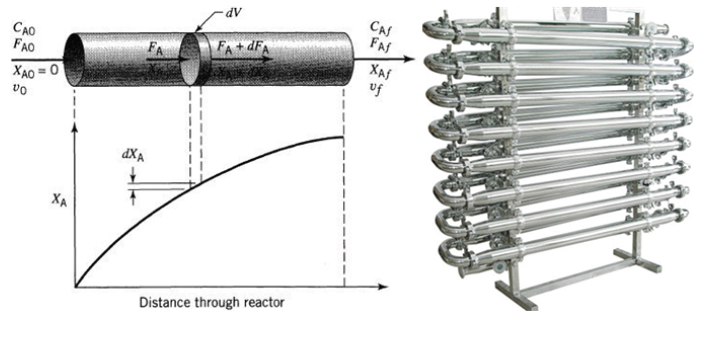
A medida que se va desplazando el reactivo a lo largo del reactor la composición va cambiando. Realizamos el balance de materia al elemento diferencial de volumen para extenderlo después a todo el reactor.
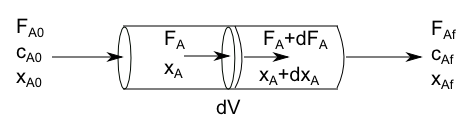
Balance de materia: Acumulación = Entrada - salida -Desaparición
- Entrada de A en el dV: $F_A$
- Salida de A del dV: $F_A+dF_A$
- Desaparición de A: $(-r_A)dV$
- Acumulación = 0
El balance de materia nos queda, $0=F_A-F_A+dF_A+(-r_a)dV$, dado que $F_A=F_{A0}(1-x_A)$, derivando obtenemos, $dF_A=-F_{A0}dx_A$. Llevando esta última ecuación al balance de materia:
\begin{equation} F_{A0}dx_A=(-r_A)dV \end{equation}
Separando variables e integrando:
\begin{equation} \int_{0}^{v}\frac{dV}{F_{A0}}=\int_{0}^{x_{Af}}\frac{dx_A}{(-r_A)} \end{equation}
La ecuación de diseño del PFR nos queda:
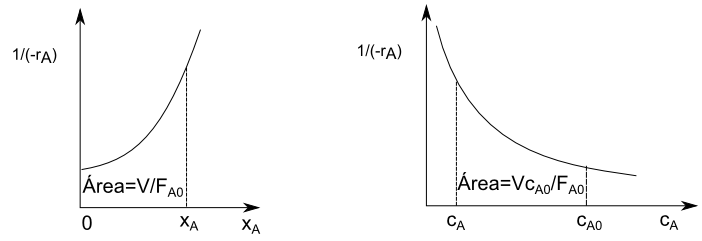
\begin{equation} \frac{V}{F_{A0}}=\int_{0}^{x_{Af}}\frac{dx_A}{(-r_A)} \end{equation}
Tambien podemos expresarla en función del tiempo espacial, teniendo en cuenta que $\tau=\frac{c_{A0}V}{F_{A0}}$
\begin{equation} \tau=c_{A0}\int_{0}^{x_{Af}}\frac{dx_A}{(-r_A)} \end{equation}
En sistemas con densidad constante $c_A=C_{A0}(1-x_a)$, derivando $dc_A=-c_{A0}dx_A$, despejando, $dx_A=\frac{dx_A}{c_{A0}}$. Sustituyendo $dx_A$ en la ecuación de diseño se obtiene:
\begin{equation} \tau=-\int_{c_{A0}}^{c_{Af}}\frac{dc_A}{(-r_A)} \end{equation}