Un horno quema gas de la siguiente composición en $\%$ en volumen: $C_2H_4=17\%$; $CH_4=21\%$; $H_2=32.9\%$; $CO=26.1\%$ $CO_2=3\%$. Tanto el gas como el aire entran a 21ºC y 1 atm, y están prácticamente secos. Los gases de combusión abandonan la chimenea a 360ºC y 0.92 atm y tienen 12.2$\%$ en volumen de $CO_2$, 0.4$\%$ de CO (ambos en base seca), además de $O_2, N_2$ y $H_2O$. calcular:
a) Los $m^3$ de aire suministrados por $m^3$ de gas.
b) El porcentaje de exceso de aire.
c) Los $m^3$ de gases de chimenea por $m^3$ de gas utilizado.
Solución:
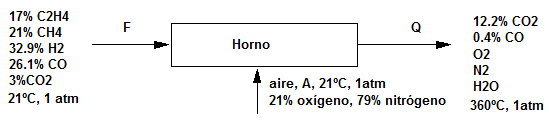
Base de cálculo: 100 moles de alimentación
Balance global parcial (carbono): $84=0.122Q+0.004Q\;\;\rightarrow\;\; Q=667.5\;moles$, en base seca.
Moles de agua producidos durante la combustión: 108.9 mol
Q=776.4 moles, en base húmeda.
Balance global parcial (nitrógeno): $1.58A=1335x_{N2}$
Balance global parcial (oxígeno): $32.1+0.42A=165.53+1335x_{O2}+108.9$
Suma de fracciones molares en Q igual a 1: $0.122+0.004+x_{O2}+x_{N2}=1$
Resolviendo el sistema obtenemos A=704.52 moles de aire
En las condiciones de la alimentación 100 moles equivalen a $2.41 m^3$.
En las condiciones de la alimentación 704.52 moles de aire equivalen a $16.98 m^3$
a) $\frac{16.98}{2.41}=7.04$volumen de aire/volumen de alimentacion
La corriente Q = 776.4 moles, equivale a un volumen de $43.804 m^3$
c) $\frac{43.804}{2.41}=18.17$ volumen de gases de chimenea/volumen de alimentación.
b) $\%oxigeno\;exceso=\frac{O_2\;entra-O_2\;requerido}{O_2\;requerido}$


